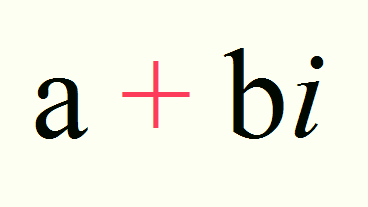【数Ⅱ】複素数の計算問題の解き方!! 相等を使えば余裕!!
今日は複素数の計算問題の解説をしていきます!!
複素数とは
複素数はa+biで表すことができて、a,bは実数、iは虚数単位です。i²=ー1(基本!!)
複素数の相等
a+bi=c+di⇔a=cかつb=d 特にa+bi=0の時a=0かつb=0 とっても重要です!!
共役な複素数
a+biとa-biを共役な複素数といいます。
それでは、これらを踏まえて練習問題にチャレンジしてみましょう。
四則演算の特に除法が少し難しいので紹介します。
結論から言うと c+di / a+bi = ac+bd / a²+b² + (ad-bc)×i / a²+b² ですが、なぜこのようになるのか説明していきます。
c+di / a+bi
=(c+di)(a-bi) / (a+bi)(a-bi)
=ac+adi-bci-bdi² / a²-b²i² i²=-1なので、
ac+bd+(ad-bc)i / a²+b² になります。この分子部分を分ければ
ac+bd / a²+b² + (ad-bc)×i / a²+b²になります。
分かりにくくてすみません。
練習問題にチャレンジ!!
(1) x+yi=2+3i (2) (x+2y)+(x-2)i=0 (3) (2i+3)x+(2-3i)y=5-i
解説
(1) 複素数の相等より、x=2、y=3
(2) 複素数の相等より、x+2y=0‥①、x-2=0‥② なので、②より、x=2.これを①に代入するとy=-1
(3) まず式をa+biの形にします。
(2i+3)x+(2-3i)y=5-i 展開すると
2ix+3x+2y-3iy-5+i=0
3x+2y-5+(2x-3y+1)i=0 複素数の相等より、3x+2y-5=0かつ 2x-3y+1=0.
この連立方程式を解くと(省略します…)x=1 y=1
チャレンジ問題
i+i²+i³+・・・+i⁵⁰
iに関する特徴を利用すれば瞬殺で解けます。
(答え)
まず、i+i²+i³+i⁴を計算してみましょう。i²=ー1なので i-1-i+1=0 となります。
50÷4=12余り2となるのでi+i²+i³+・・・+i⁵⁰=i⁴⁹+i⁵⁰ と変形できます。周期の前二つの値はi-1なので、答えはi-1です!!!
どうですか??複素数の計算問題は複素数の相等を使えば楽々解けるので、苦手意識を頑張って変えましょう!!
ご覧いただきありがとうございました。
ぜひほかの記事も見ていってください!